| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Recoil
- docker
- react
- 정규표현식
- component
- Redux
- Modal
- 포트포워딩
- styled-component
- 성능최적화
- javascript animation
- npx
- go
- 웹팩
- socket.io
- 반응형웹
- graphql
- AWS
- route
- CDN
- express
- sequelize
- typescript
- 웹크롤링
- cicd
- scrapping
- 회고
- Today
- Total
프로그래밍 공부하기
자료구조 6. Priority Queue(Heap) 본문
[자료구조 포스팅]
1. Priority Queue
일반적인 Queue와 달리 데이터를 출력할 때 입력 순서와 상관없이 우선순위가 높은 데이터를 먼저 출력하는 Queue가 Priority Queue이다. 우선순위 큐는 보통 Heap 자료구조로 구현하며, 우선순위가 있는 작업, 예를 들면 운영체제의 작업스케줄러(SJF/최단작업우선스케줄링 등)에 사용된다.

우선순위 큐를 Heap으로 구현하는 이유는 무엇일까? Priority Queue를 선형자료구조(큐, 스택, 연결리스트)에 저장할 경우 데이터 입출력 시 데이터의 우선순위에 따라 Queue에 존재하는 데이터들이 한 칸씩 밀리거나 당겨지는 일이 발생할 수 있다. 예를 들어 값이 클수록 우선순위가 높은 숫자들을 저장해야한다고 생각해보자. 위와 같이 선형으로 숫자들을 저장한 뒤 6를 입력하면 어떻게 될까? 6이 들어갈 찾기 위해 저장소의 각 요소를 차례대로 접근해야 하며, 삽입 시, 6보다 작은 요소들은 모두 한 칸씩 뒤로 이동시켜야 한다. 시간복잡도는 O(n)이다.

Heap은 완전 이진트리의 일종으로, 우선순위에 따라 부모 노드와 자식 노드 간 정렬이 되어있어 우선순위가 가장 높은 노드를 빨리 찾을 수 있는 자료구조이다. 값이 클수록 우선순위가 높은 경우 최대 힙(max heap)이라 부르며 부모노드가 항상 자식노드보다 크거나 같다. 따라서 힙의 최상위 노드(root)는 가장 큰 값이다. (단, 형제 노드끼리는 정렬되지 않으므로 Binary Search Tree는 아니다.)
같은 데이터를 저장한 힙(위 그림)에서 6을 입력해보자. 일단 6은 가장 하위 레벨(5의 자식)으로 입력된다. 그 후 부모인 5와 비교하여 6이 더 크므로 부모와 자리를 교환한다. 이 후 다시 9와 비교하여 9보다 작으므로 자리가 고정된다. 이 때 이전과 다른 점은 [1, 3, 8]과는 비교하지 않는다는 점이다. 힙은 직접 연결된 부모-자식간의 값만 비교하므로 부모의 형제를 루트로 하는 부분트리의 노드와는 비교하지 않는다. 시간복잡도로 따지면 O(log2N)이다.
2. Priority Queue 구현
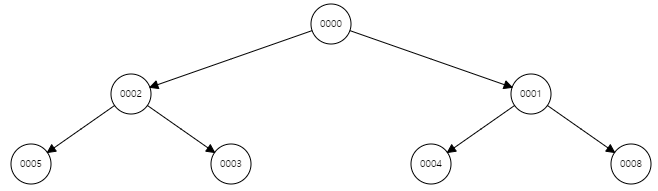
최소 힙을 구현해보자. 최소 힙은 작을 수록 높은 우선순위를 가지므로, 루트의 값이 항상 가장 작은 값이다. 위 최소 힙은 위의 트리는 [0, 2, 1, 5, 3, 4, 8] 이라는 배열과 동일하다.
2-1. 요소를 추가할 때

새로운 요소가 추가되면 우선 가장 트리의 가장 마지막으로 넣어진다. 그 후 부모노드와 비교해서 작으면 부모와 위치를 교환하고, 이를 반복해나간다.
노드의 자식은 2개까지 가질 수 있다. 따라서 n번째 노드의 부모는 Math.floor((n-1) / 2) 와 동일하다. 예를 들어 배열 인덱스가 0부터 시작하고 값이 [0, 1, 2]일 때 최상위 노드는 0이며, 자식으로 1과 2를 갖는다. 0 = f(1) = f(2) 를 만족시켜야 하므로 f(n) = Math.floor((n-1)/2) 이다.
function swap(idx1, idx2, arr) { //두 값을 교환
[arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
}
function getParentIdx(idx) { //배열은 0부터 시작
return Math.floor((idx - 1) / 2);
}
function insert(heap, item) {
//1. 일단 넣고 부모 index를 계산한다.
let idx = heap.length;
let parentIdx = getParentIdx(idx);
heap.push(item);
//2. 부모와 비교해서 작으면 부모와 교환하는 것을 반복한다.
while (item < heap[parentIdx]) {
swap(idx, parentIdx, heap);
idx = parentIdx;
parentIdx = getParentIdx(idx);
}
return heap;
}코드로 구현하면 위와 같다. insert()구현 전에 heap의 두 노드의 값을 교환하는 swap()과 부모노드의 인덱스를 계산하는 getParentIdx를 구현하여주었다. 그 후 Insert는 쉽게 구현할 수 있다.
2-2. 요소를 제거할 때

루트노드를 제거한 경우 우선 가장 마지막 노드의 값이 루트노드의 값으로 변경된다. 그 후 자식 중 더 작은 값과 계속 비교해서 해당 값이 더 크다면 자식요소와 교환하고 이를 반복해나간다. 자식 노드는 부모노드와 반대로 n*2 + 1로 구하며, 두 자식 노드 중 더 작은 노드와 값을 비교하고 교환해나간다.
function getLeftChildIdx (idx){
return idx * 2 + 1;
}
function removeRoot(heap) {
//1. 가장 끝에있는 요소가 루트로 간다.
swap(0, heap.length - 1, heap);
heap.pop();
if (heap.length === 0)
return [];
let idx = 0;
let leftIdx = getLeftChildIdx(idx);
let rightIdx = leftIdx + 1;
//2. 자식 둘 중에 더 작은 값이랑 계속 비교해나간다.
while (heap[idx] > heap[leftIdx] || heap[idx] > heap[rightIdx]) {
let childIdx = heap[leftIdx] > heap[rightIdx] ? rightIdx : leftIdx;
swap(idx, childIdx, heap);
idx = childIdx;
leftIdx = getLeftChildIdx(idx);
rightIdx = leftIdx + 1;
}
return heap;
}
2-3. 힙정렬
const binaryHeap = function (arr) {
return arr.reduce((heap, item) => {
return insert(heap, item);
}, []);
};
const heapSort = function (arr) {
let minHeap = binaryHeap(arr);
const sorted = [];
while (minHeap.length > 0) {
sorted.push(minHeap[0]);
minHeap = removeRoot(minHeap);
}
return sorted;
};힙정렬은 최소 힙을 이용한 정렬이다. 최소 힙의 루트 노드는 가장 작은 수이다. 따라서 배열을 정렬하기 위해 먼저 계속 배열의 요소들을 insert해나가 최소 힙을 만든 후에 최소 힙의 루트 노드를 계속 pop하면 오름차순으로 정렬된 배열을 얻을 수 있다.
Heap은 우선순위가 있는 데이터를 다룰 때 유리하다. 야근지수(Programmers)와 같은 문제에서 이를 활용할 수 있다.
gif출처: www.cs.usfca.edu/~galles/visualization/Heap.html
'Algorithm' 카테고리의 다른 글
| [Programmers] 징검다리 건너기 (0) | 2021.06.28 |
|---|---|
| [Programmers] 가장 긴 팰린드롬 (0) | 2021.06.25 |
| [Programmers]최고의 집합 (0) | 2021.05.28 |
| [Programmers]야근 지수 (0) | 2021.05.27 |
| [Programmers]하노이의 탑 (0) | 2021.05.26 |



