| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 성능최적화
- CDN
- AWS
- 정규표현식
- 포트포워딩
- npx
- graphql
- docker
- express
- sequelize
- 웹크롤링
- cicd
- 웹팩
- socket.io
- typescript
- component
- go
- 회고
- Recoil
- javascript animation
- 반응형웹
- Redux
- route
- styled-component
- Modal
- react
- scrapping
- Today
- Total
프로그래밍 공부하기
자료구조 4. Graph 본문

1. Graph
자료구조에서 그래프란 정점(vertex, node)과 정점 사이를 연결하는 간선(edge)으로 구성된 자료구조이다. 그래프는 간선의 방향유무에 따라 무방향 그래프와 방향 그래프로 나뉜다. 간선은 보통 간선이 연결하고 있는 두 정점의 쌍으로 표시하며 무방향 그래프의 경우 괄호를 사용하여 (A, B), 방향 그래프의 경우 꺽쇠 기호를 사용하여 <A, B>와 같이 표기한다. 그 외에 간선에 비용이나 가중치가 할당된 가중치 그래프(weighted graph)가 존재한다.
2. 용어
그래프와 관련된 다양한 용어들이 존재한다. 이러한 용어들을 하나씩 알아보자.
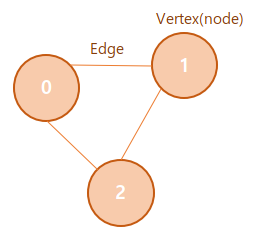
- Vertex(정점): 그래프의 각 정점을 vertex 혹은 node라고 한다. 위 그래프에서는 0, 1, 2 총 3개의 노드가 존재한다.
- Edge(간선): 노드와 노드 사이를 이어주는 선을 간선이라 한다. 위 그래프에서는 총 3개의 간선이 존재한다.
- complete graph(완전 그래프): 그래프 상의 모든 정점들 사이에 직접 연결된 간선이 존재하는 그래프이다. 즉, 간선의 수가 최대인 그래프를 의미한다. 위 그래프는 완전 그래프이다.
- n개의 정점을 가진 무방향 그래프는 간선 수가 n*(n-1) / 2 인 경우 완전 그래프이다.
- n개의 정점을 가진 방향 그래프는 간선 수가 n*(n-1)인 경우 완전 그래프이다.
- subgraph(부분 그래프): 원본 그래프의 일부인 그래프를 부분 그래프라 한다. 부분 그래프의 정점과 간선은 원래 그래프의 정점과 간선의 부분 집합이다.
- adjacent(인접): 무방향 그래프에서 정점 A, B 사이에 간선이 존재한다면 정점 A는 정점 B에 인접한다.
- incident(부속): 무방향 그래프에서 정점 A, B 사이에 간선이 존재한다면 간선 (A, B)는 정점 A, B에 부속한다.

G2는 G1의 subgraph이다. - trail(경로): 정점 A에서 정점 B로 가는 경로. 이미 사용된 간선은 다시 사용하지 않는다.
- circuit(회로): 출발점과 도착점이 같은 경로(closed trail)
- path(경로): 정점 A에서 정점 B로 가는 경로. 이미 사용된 간선과 정점은 다시 사용하지 않는다.
- cycle(사이클): 출발점과 도착점이 같은 경로(closed path)
- circuit(회로): 출발점과 도착점이 같은 경로. 이미 사용된 간선을 재사용 가능하다
- degree(차수): 정점에 부속(incident)된 간선의 수
- in-degree(진입차수): 정점을 향해 들어오는 방향의 간선의 수
- out-degree(진출차수): 정점으로부터 나가는 방향의 간선의 수
3. 그래프 표현
1) adjacency matrix

그래프를 이차원 행렬(인접행렬)을 이용하여 표현하는 방법이다. 무방향 그래프의 인접행렬은 대각선의 방향으로 서로 대칭인 구조를 갖고 있다. 위 그래프와 인접행렬을 살펴보면 0번 정점은 정점 1과 2와 연결이 되어있으므로 1로 표시하고 3번 저점와는 연결이 되어 있지 않으므로 0으로 표시한다.
인접행렬로 구현할 경우 배열에 그래프 간선 정보가 저장되므로 두 정점의 연결유무를 빠르게 조회할 수 있으며(O(1)) 구현이 비교적 간단하다. 반면, 모든 간선에서 모든 간선에 대한 정보를 2차원 배열에 저장하므로 구현 시 O(n²)의 시간 복잡도를 갖는다. 또한 간선이 없다는 정보도 따로 저장해야하며, 무방향 그래프의 경우 간선 정보가 2번 저장되게 된다(대각선 대칭). 따라서 필요 이상의 공간이 낭비된다.
2) adjacency lists

그래프를 인접 리스트로 표현하는 방법이다. 각 정점에 대해 정점에 인접한 다른 정점들을 하나의 리스트에 담아 저장하는 것이다. 리스트는 공간을 동적으로 할당하므로 공간 활용도가 높다는 장점이 있다. 반면 리스트를 사용하기 때문에 두 정점의 연결유무를 확인하기 위해 배열보다 오랜 시간(O(n))이 소모된다. 또한 구현이 배열에 비해 비교적 어렵다.
4. 구현
class Graph {
constructor() {
this.nodes = {};
}
addNode(node) {
this.nodes[node] = this.nodes[node] || [];
}
contains(node) {
return Object.keys(this.nodes).includes(`${node}`);
}
removeNode(node) {
for (let key in this.nodes) {
this.removeEdge(key, node);
}
delete this.nodes[node];
}
hasEdge(fromNode, toNode) {
if (this.nodes[fromNode] === undefined || this.nodes[toNode] === undefined) {
return false;
} else {
return this.nodes[fromNode].includes(toNode);
}
}
addEdge(fromNode, toNode) {
this.nodes[fromNode].push(toNode);
this.nodes[toNode].push(fromNode);
}
removeEdge(fromNode, toNode) {
let index1 = this.nodes[fromNode].indexOf(toNode);
if (index1 !== -1) {
this.nodes[fromNode].splice(index1, 1);
}
let index2 = this.nodes[toNode].indexOf(fromNode);
if (index2 !== -1) {
this.nodes[toNode].splice(index2, 1);
}
}
}
참고 사이트
[Algorithm] 자료구조 그래프(Graph)란 무엇인가?
그래프란? 그래프는 정점과 간선으로 이루어진 자료구조입니다. 정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼수도 있겠습니다. 그런면에서 트리는 그래프의 일종인 셈입니다. 다만
coding-factory.tistory.com
What is difference between cycle, path and circuit in Graph Theory
I am currently studying Graph Theory and want to know the difference in between Path , Cycle and Circuit. I know the difference between Path and the cycle but What is the Circuit actually mean.
math.stackexchange.com
'Algorithm' 카테고리의 다른 글
| 문제풀이 코드 Git 주소 (0) | 2021.01.25 |
|---|---|
| 자료구조 5. Tree (0) | 2021.01.22 |
| 자료구조 3. Hash Table (0) | 2021.01.21 |
| 자료구조 2. Linked List (0) | 2021.01.21 |
| 자료구조 1. Stack, Queue (0) | 2021.01.19 |



