| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- route
- 회고
- 반응형웹
- Recoil
- AWS
- typescript
- socket.io
- CDN
- component
- sequelize
- express
- graphql
- 성능최적화
- npx
- react
- 정규표현식
- scrapping
- styled-component
- Redux
- 포트포워딩
- Modal
- docker
- 웹크롤링
- 웹팩
- javascript animation
- go
- cicd
- Today
- Total
프로그래밍 공부하기
[Programmers]하노이의 탑 본문
코딩테스트 연습 - 하노이의 탑
하노이 탑(Tower of Hanoi)은 퍼즐의 일종입니다. 세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대
programmers.co.kr
하노이의 탑은 재귀를 연습할 수 있는 유명한 문제이다. 하노이의 탑을 통해 재귀를 찾고 JS 코드로 구현해보자.
1. 재귀
1. 큰 문제를 더 작은 문제로 계속 나눈다.
2. 가장 작은 문제를 해결한다.
3. 가장 작은 문제의 해결을 이용하여 큰 문제를 해결해나간다.
일반적으로 재귀함수는 위와 같은 형식으로 문제를 해결한다. 이를 코드로 나타내면 다음과 같다.
function recursive(input1, input2, ...) {
// 재귀의 기초 (base case)
if (문제를 더 이상 쪼갤 수 없을 경우) {
return 단순한 문제의 해답;
}
// recursive Case(복잡한 문제)
return 더 작은 문제로 새롭게 정의된 문제 //ex. return input1 + recursive(input2-1)
}우선 가장 작은 문제를 재귀함수의 가장 상단에 if문으로 작성한 후 답을 리턴한다. 재귀함수의 input이 가장 작은 문제가 아닌경우 더 작은 문제로 나누어 재귀함수를 다시 리턴한다. 따라서 재귀함수로 문제를 해결하기 위해선 문제를 어떻게 정의하고 가장 작은 케이스를 찾는 것이 중요하다.
2. 하노이의 탑 관찰

하노이의 탑은 1번 막대에 있는 원반들을 3번 막대로 모두 이동시키는 문제이다. 하노이의 탑 문제를 재정의하기 위해 하노이의 탑을 관찰해보자.

하노이의 탑에서 가장 작은 케이스는 원반이 1개인 경우이다. 1에 있던 원반을 바로 목적지인 3으로 옮긴다.

위 케이스는 원반이 2개인 경우이다. 문제를 풀기 위해선 가장 큰 원반이 먼저 3번에 있어야 한다. 따라서 가장 작은 원반을 2로 옮겼다. 그 후 가장 큰 원반을 3번으로 옮기고 2번 원반을 3번으로 옮겨주었다. N = 1인 케이스로 이 과정을 설명할 수 있을까? 아직은 잘 안보일 수 있다. N = 3인 경우를 보자.
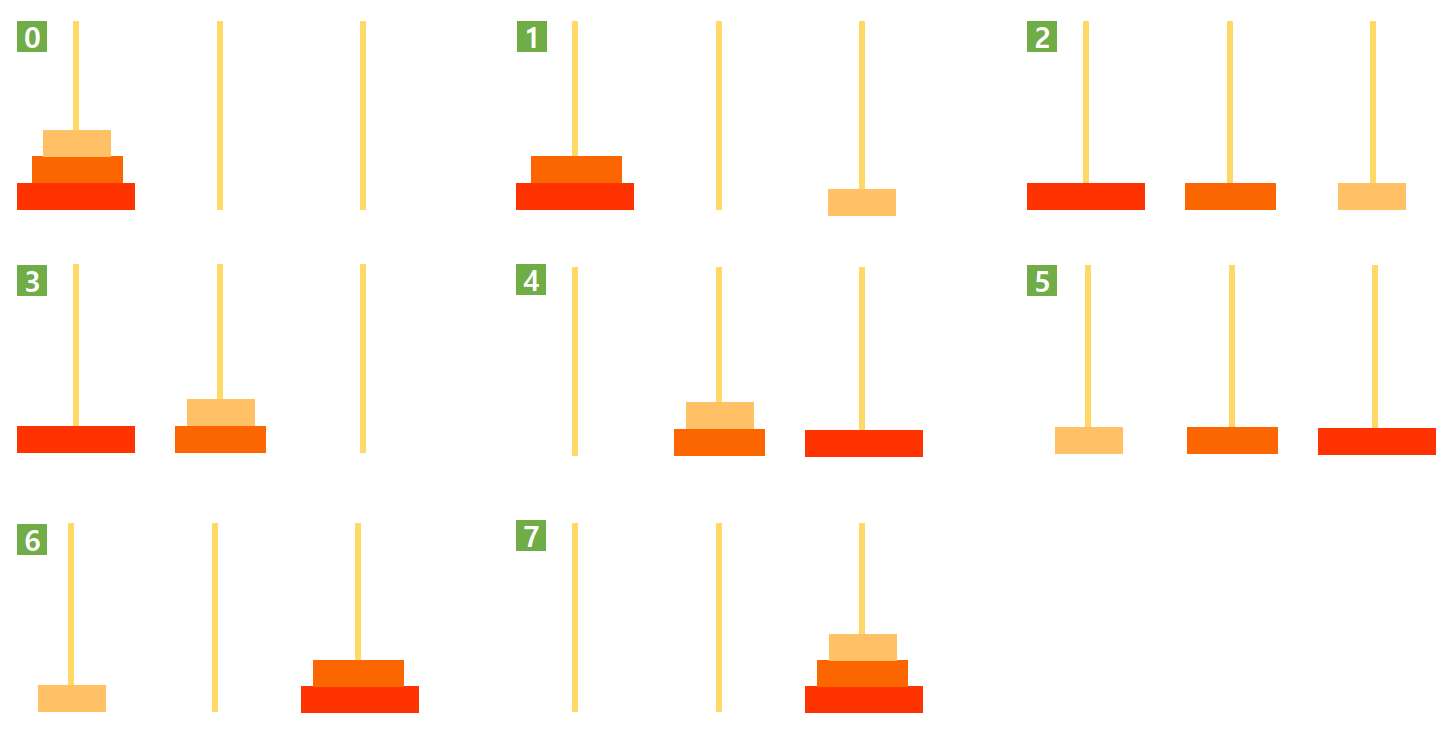
N = 3인 경우는 위와 같다. N = 2인 경우로 위의 해답을 만들어낼 수 있을까? N = 3에서도 역시 먼저 가장 큰 원반을 3번으로 옮겨야 한다. 이를 위해선 2개의 원반을 2번으로 옮겨야 한다(과정 1-3). 다음으로 가장 큰 원반을 3번으로 옮긴다. 그 후 2번에 있는 2개의 원반을 3번으로 옮긴다(과정 4-7). 3개의 원반을 옮기는 문제에는 2개의 원반을 옮기는 문제 2가지와 가장 큰 원반을 옮기는 문제가 포함되어있는 것이다. 이제 N개의 원반으로 이를 표현해보자.
[N개의 원반 옮기기]
1. N-1개의 원반을 1번에서 2번으로 옮긴다.
2. 가장 큰 원반을 1번에서 3번으로 옮긴다.
3. 2번에 있는 N-1개의 원반을 2번에서 3번으로 옮긴다.
정의된 1-3을 보면 각 문제가 N 뿐만 아니라 출발지와 도착지가 다른 것을 알 수 있다. 즉, 재귀함수의 매개변수로 N과 출발지, 도착지의 정보가 필요하다. 또한 N개의 원반을 옮길 때로 보았을 때 결국 1번, 2번, 3번 막대를 모두 사용하게 되므로 경유지 정보도 필요하다. 예를 들어 N개의 원반을 옮길 때 크게보면 1번은 출발지, 3번은 도착지, 2번은 경유지가 되며, 문제를 쪼개 N-1개의 원반으로 봤을 때(1번 단계)는 1번이 출발지, 2번지 도착지, 3번이 경유지가 된다.
3. 코드
function solution(n) {
const answer = [];
const aux = (N, start, end, mid) => {
if (N === 1) { //가장 작은 경우
answer.push([start, end]);
return;
}
aux(N - 1, start, mid, end); //N-1을 1번에서 2번으로 옮기기
answer.push([start, end]); //가장 큰 원반 3번으로 옮기기
aux(N - 1, mid, end, start); //N-1을 2번에서 3번으로 옮기기
}
aux(n, 1, 3, 2);
return answer;
}코드로 표현하면 위와 같다. solution 함수 내에는 하노이의 탑을 해결하는 aux라는 재귀함수가 포함되어있다. aux에서는 먼저 가장 작은 경우인 N = 1인 경우의 해답을 적고 N = 1에 도달하면 return으로 재귀를 멈춘다. 그 외의 경우는 위에서 정의한 대로 N, 출발지, 도착지, 경유지의 정보가 다른 재귀함수를 부르고 가장 큰 원반을 옮기는 작업을 수행한다.
'Algorithm' 카테고리의 다른 글
| [Programmers]최고의 집합 (0) | 2021.05.28 |
|---|---|
| [Programmers]야근 지수 (0) | 2021.05.27 |
| 빈 문자 접근: 숫자 인덱스와 charAt 방식 (0) | 2021.05.13 |
| Dijkstra 알고리즘 (0) | 2021.05.11 |
| Heap (0) | 2021.05.01 |


