Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 포트포워딩
- typescript
- graphql
- 웹팩
- scrapping
- Modal
- react
- 웹크롤링
- docker
- AWS
- 정규표현식
- 성능최적화
- cicd
- express
- styled-component
- socket.io
- Redux
- 반응형웹
- javascript animation
- CDN
- Recoil
- component
- npx
- 회고
- route
- go
- sequelize
Archives
- Today
- Total
프로그래밍 공부하기
Dijkstra 알고리즘 본문
무방향 그래프의 한 정점(start)에서 다른 정점(end)까지 최단거리를 찾는 함수를 작성하세요.
입출력 예시
let num = 4;
let edges = [ [1, 2, 6], [1, 3, 2], [2, 3, 3], [2, 4, 1], [3, 4, 5], ];
let start = 1;
let end = 4;
Dijkstra(num, edges, start, end); // 6 (1 - 3 - 2 - 4)
그래프에서 노드 간의 최단 경로를 찾는 대표적인 알고리즘 중 하나가 다익스트라 알고리즘이다. 위 문제를 다익스트라 알고리즘을 통해 풀어보자. 우선 다익스트라 알고리즘은 다음과 같은 순서로 진행된다.
- 시작점과 모든 노드와의 거리(비용)를 기록한다.
- 시작점과 연결된 모든 노드 중 가장 최단거리인 노드(A) 및 간선을 찾는다.
- 찾은 간선을 거쳐 A 노드에 도달하였을 때 원래 시작점에서 A 노드로의 직선경로보다 빠르다면 시작점과 A 노드와의 거리를 갱신한다.
- 방문하지 않은 노드(A 제외한 노드) 중 최단 거리인 간선을 찾아 2-3 과정을 반복한다.
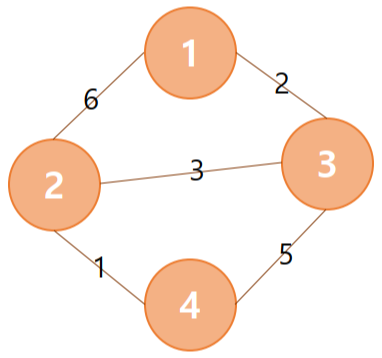
예를 들어 위의 그래프의 1번 노드에서 4번 노드까지의 최단거리를 구하는 과정은 다음과 같다.

1) 1번 노드와 모든 노드와의 거리를 기록한다. 연결되지 않거나 자기 자신은 INF(Infinity)로 표시한다.

2) 1번 노드와 연결된 노드 중 가장 최소 거리인 노드는 3번 노드이다. 따라서 3번을 거쳐 다른 노드로 갔을 때의 거리를 계산하고 해당 값이 더 작다면 거리 기록을 갱신한다.
- '1번 -> 3번 -> 2번' 경로는 거리 5로 '1번 -> 2번' 경로의 거리 6보다 짧으므로 갱신된다.
- '1번 -> 3번 -> 4번' 경로는 거리 7로, '1번 -> 4번' 경로의 거리 INF보다 짧으므로 갱신된다.

3) 방문한 3번을 제외하고 가장 가까운 노드는 2번이다. 따라서 2번을 거쳐 다른 노드로 갔을 때 거리를 계산하고 해당 값이 더 작다면 거리 기록을 갱신한다.
- '1번 -> 3번 -> 2번 -> 4번' 경로는 거리 6으로 '1번 -> 3번 -> 4번' 경로의 거리 7보다 짧으므로 갱신된다.
4) 4번 노드를 거치는 경우 더 짧은 경로가 없으므로 갱신되지 않는다.
5) 따라서 출발 노드(1번)에서 도착 노드(4번) 까지의 최소 거리는 6이다.
위 과정을 코드로 나타내면 다음과 같다.
function createGraphByMatrix(num, edges) {
const matrix = [];
const INF = Number.MAX_SAFE_INTEGER; //보통 문제에서 주어진 최대 거리 + 1 을 넣는다.
for (let row = 0; row <= num; row++) {
matrix.push(Array(num + 1).fill(INF));
}
edges.forEach(([src, dst, weight]) => {
matrix[src][dst] = matrix[dst][src] = weight;
});
return matrix;
}
function Dijkstra(num, edges, start, end) {
const isVisited = Array(num + 1).fill(false); //방문한 노드인가
const matrix = createGraphByMatrix(num, edges); //2차원 배열로 그래프 변환
const dist = matrix[start].slice(); //시작지점과 다른 노드와의 거리 저장할 변수
const getSmallIndex = (row) => { //가장 가까운 노드의 인덱스 찾기
let maxIdx = 0;
for (let i = 1; i < row.length; i++) {
if (row[maxIdx] > row[i] && isVisited[i] === false) maxIdx = i;
}
return maxIdx;
}
isVisited[start] = true;
for (let step = 0; step < num - 2; step++) { //출발지, 도착지 제외하므로 -2
const nearest = getSmallIndex(dist); //최소비용 노드 가져오기
isVisited[nearest] = true; //방문하기
for (let j = 0; j < num + 1; j++) {
//선택된 노드를 거쳤을 때 더 짧은 거리가 나온다면 갱신한다.
if (!isVisited[j] && dist[nearest] + matrix[nearest][j] < dist[j]) {
dist[j] = dist[nearest] + matrix[nearest][j];
}
}
}
return dist[end];
}
'Algorithm' 카테고리의 다른 글
| [Programmers]하노이의 탑 (0) | 2021.05.26 |
|---|---|
| 빈 문자 접근: 숫자 인덱스와 charAt 방식 (0) | 2021.05.13 |
| Heap (0) | 2021.05.01 |
| 문제풀이 코드 Git 주소 (0) | 2021.01.25 |
| 자료구조 5. Tree (0) | 2021.01.22 |
Comments


